Solving Inequalities Using a Numberline

This series of 3 minute math is designed as a quick reminder for some of the main topics, including solving inequalities using a numberline. I hope they help to provide a focus and a way forward. If you need any more detail please search the site or contact me – always pleased to answer any questions!

All the very best with your studies.

Where are inequalities used?

In the UK you need to be over the age of 17 to have a licence to drive a car. This could be written as an inequality:

Age ≥ 17

In other words you have to be older than, or equal to, 17 to drive.

Inequalities can get a little more complicated and, at GCSE, tend to be given with two variables. As an example, if you had £60 to spend and wanted to buy some T shirts (£3 each) and jeans (£17 each).

Let ‘x’ be the number of T shirts and ‘y’ be the number of jeans. The amount of money to be spent is less than or equal to £60. The equation would look like this:

3x+17y ≤ 60

 

Video Transcript

“Welcome to 3 Minute Maths. In this particular video, we’re going to looking at solving inequalities using a numberline. This is usually a grade 4 type of question. The way it will be presented will be something like:

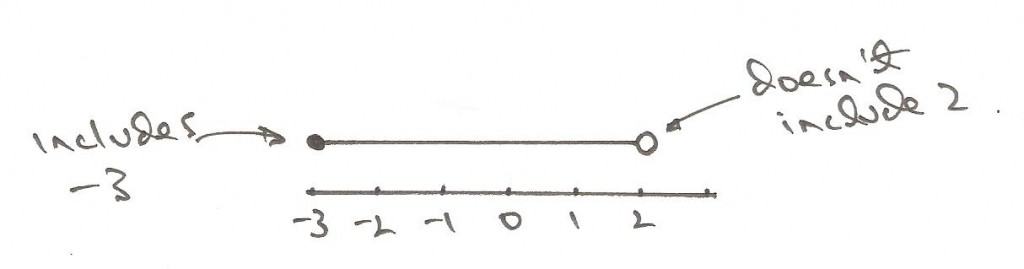
-3  ≤ x < 2

You look at that and think “I don’t know where I’m going to start with that”. Well, it’s fairly straightforward providing that you follow some of the rules.

One of the ways to look at it is a numberline. We have the two values (-3 and 2) and what we’re looking for is the solutions to x between those two values. What I’ll do is start by making a line and placing -3, then -2, -1, 0, 1, 2. So, that’s -3 through to 2.

Draw a line between the two values and then a circle on both ends. Use a closed circle if the inequality includes -3.

If the circle is open, it doesn’t include the value. This means x is not 2, it’s less than 2.

In this particular case, -3 is equal to x and the value of x could be -3 so we leave that as a closed circle.

To solve this, we look at what we call ‘integer (or whole number) solutions’ and this is the way the question would be worded as. So, in this particular case, the whole numbers would be -3 (I can include -3 because the circle is closed), -2, -1, 0, and 1, but not 2. The integer 2 is not included.

I hope that’s been okay for you. Please do have a look at some of the other videos in the series and also some of the application of inequalities, which I cover in some of the other videos. I hope that’s been helpful and I’ll look forward to seeing you inside the next video.”

Watch this video on YouTube.

Here’s another post that might be of interest:

Solving inequalities using algebra

Inequalities on a graph